For the base of the swimming pool:
You have the next figures as the sides:
The side number 1 and side 2 are retangles:

For the sides 3 and 4 you can draw the side as the sum of a recrtangle and a triangle:
Then, the area of this sides is the sum of the area of the rectangle and the area of the triangle:
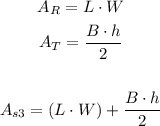
You have the next figure as the base:
The area of a rectangle is:
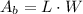
L is length and w is width
To find the lenght you use the trangle formed in the side 3 and 4:
Pythagoras theorem:
![\begin{gathered} x=\sqrt[]{0.7^2+25^2} \\ x=\sqrt[]{0.49+625} \\ x=\sqrt[]{625.49} \\ x=25.01m \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4wcy64gurce166zx8kmtdl4nxnrd4o3679.png)
Then, you have the next areas:Side 1:
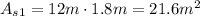
Side 2:

Side 3:
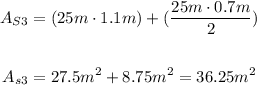
Side 4:
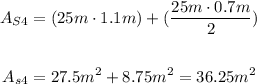
Base:
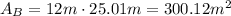
The total area of the swimming pool is the sum of the areas above, approx. 407 sqare meters