The height of the radio tower is 327.3070 feet.
Step-by-step explanation
Let's first sketch the problem.
From the sketch above, adjacent = 46 θ=82
opposite = h (height of the radio tower.
Using the trigonometric ratio,
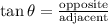
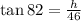
Cross-multiply
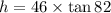
h ≈ 327.3070 feet.
Therefore, the height of the radio tower is 327.3070 feet.