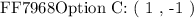We will investigate the relevance of inverse of a function.
A function is usually defined as a relationhsip between the input variable and output. It relates the two variables in form off an elgebraic expression. For every value of input ( x ) their is a unique value of the output this qualifies as a definition of a function.
We are given the following function as follows:
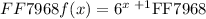
Where,
![\begin{gathered} f\text{ ( x ) : Output ( dependent variable )} \\ x\colon\text{ Input ( Independent variable )} \end{gathered}]()
Next we will go ahead an define an inverse of a function. The term inverse is given to a transformation of any line or a graph undergoing reflection. Strictly, speaking in terms of a function an inverse is:
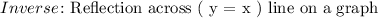
The above expression says that an inverse of any function is a reflection of the entire graph across the ( y = x ) line on a 2D cartesian coordinate system.
Mathematically evaluating the reflection across any line we will follow the guidelines:
Step 1: Interchange of input and out variables
This step basically means that when we look at our given function f ( x ) we have two variables i.e Independent variable ( x ) and dependent variable ( f (x) ). We will interchange these with each other using the following relation of reflection:
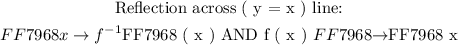
We will use the above two relations highlighted in red and do the following:

Step 2: Make the inverse notation subject of the equation
Once we have interchanged the vairables we will make f^-1 ( x ) the subject of an equation by first taking natural logs on both sides ( Ln ) as follows:
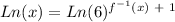
Next we will use the natural log base law as follows:

Apply the above law to the right hand side of the latest expression formed above:
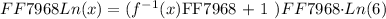
Now we will divide the Ln ( 6 ) on both sides of the equation as follows:
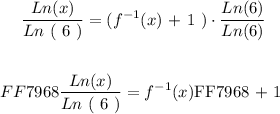
We will now subtract ( 1 ) on both sides as follows:
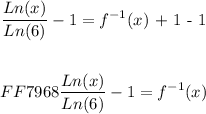
The above expression is the final expression for an inverse of a function. The inverse of the given function is:
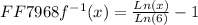
Now we will investigate what point will lie on the inverse of the function graph. Before we go to that we will recall some properties of a Natural Log as follows:

The above is the most important property of a natural log. This means for any values of ( x ) less than ( 1 ) the function is undefined or there is no such point!
Using the above property we will rule out most of our option choices as follows:

Now we will check about option ( C ) whether the point satisfies our inverse relationship or not as follows:

Therefore, the last option ( C ) lies on the inverse of the given function: