Question

hi i learned this in the beginning of the year and i don’t remember how to solve it or find restrictions. Please help

Answer 1

B. x = 10

C. x = -10

Explanation:

We have the following equation:

`(5x)/(4x+40)+(x+100)/(6)=(30)/(x^2-100)`

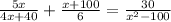
To determine the domain, we must know that it is the set of input values of a function, in this case they would be the values that x can take.

Because it is a rational equation, the denominator cannot be equal to 0, therefore, we set the corresponding denominators equal to 0 as follows:

`\begin{gathered} 4x+40=0 \\ \\ \text{ we solve for x:} \\ \\ 4x=-40 \\ \\ x=(-40)/(4)=-10 \\ \\ \\ x^2-100=0 \\ \\ x^2=100 \\ \\ x=√(100) \\ \\ x=\pm10 \end{gathered}`

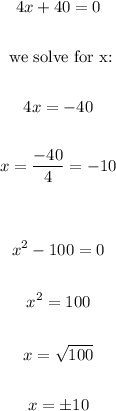
This means that the domain is equal to all the real ones except when x is equal to 10 and -10, that is, those would be the restrictions of the domain.

Therefore, the correct answer is B. x = 10 and C. x = -10