Question

You have deposited the other $400 in a savings account, which pays three percent interest compounded quarterly. Find the amount in the account for 0, 5, 10, 15, and 20 years, using the compound interest formula.

Answer 1

The compound interest formula is given by:

`I=P(1+(r)/(n))^(tn)`

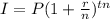
where,

P: principal investment = $400

r: interest rate = 3% = 0.03

n: times at year = 4 quarterly

t: years = 0, 5 , 10, 15, 20

Replace the previous values of the parameters into the formula for I and simplify for each value of t:

`\begin{gathered} I_0=400(1+(0.03)/(4))^(0\cdot4)=400(1+0.0075)^0=400(1.0075)^0=400 \\ I_5=400(1.0075)^(5\cdot4)\approx464.5 \\ I_(10)=400(1.0075)^(10\cdot4)\approx539.3 \\ I_(15)=400(1.0075)^(15\cdot4)\approx626.3 \\ I_(20)=400(1.0075)^(20\cdot4)\approx727.2 \end{gathered}`

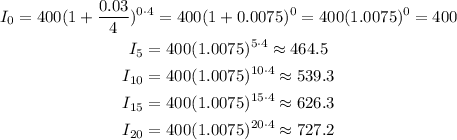
Hence, the amounts for t=0, 5, 10, 15 and 20 years are, respectivelly:

$400

$464.5

$539.3

$626.3

$727.2