see the figure below to better understand the problem
step 1
Find out the resultant vector in the x-coordinate
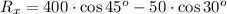
![R_x=400\cdot\frac{\sqrt[]{2}}{2}-50\cdot\frac{\sqrt[]{3}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/rrjwg3h02wxw0l697owgxq45f9pb92772o.png)
![\begin{gathered} R_x=200\sqrt[]{2}-25\sqrt[]{3} \\ R_x=239.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/p87pemj39vor4rokoydgiv8b164jqcotk7.png)
step 2
Find out the resultant in the y-coordinate
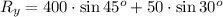
![R_y=400\cdot\frac{\sqrt[]{2}}{2}+50\cdot(1)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/bt0mgcdsosbid00nc7ljeapx0ic9sbafzq.png)
![\begin{gathered} R_y=200\cdot\sqrt[]{2}+25 \\ R_y=307.8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nl474jradu797jphkaacvkiox0miqtau2x.png)
step 3
Find out the angle of the resultant
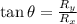
![\tan \theta=\frac{200\cdot\sqrt[]{2}+25}{200\sqrt[]{2}-25\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/9e57qtjljal9qgrtrwpd8cgrca9armksv3.png)
simplify
![\tan \theta=\frac{25\lbrack8\cdot\sqrt[]{2}+1\rbrack}{25\lbrack8\sqrt[]{2}-\sqrt[]{3\rbrack}}](https://img.qammunity.org/2023/formulas/mathematics/college/sg5tfh9830ilmclxwwoae79n6uwo7z2zok.png)
![\begin{gathered} \tan \theta=\frac{8\cdot\sqrt[]{2}+1}{8\sqrt[]{2}-\sqrt[]{3}} \\ \theta=52.1^o \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rpgi2rkboe10j6u1apf29xazmjy8ymq38o.png)
Find out the resultant vector
![R=\sqrt[]{Ry^2+Rx^2}^{}_{}](https://img.qammunity.org/2023/formulas/mathematics/college/jffwojr2kurw20wl92kncnkvygand78zna.png)
![\begin{gathered} R=\sqrt[]{307.8^2+239.5^2} \\ R=390\text{ }(km)/(h) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wcr926d8wq8xoxi8g8wz3uxi63anruqowj.png)
therefore
The resultant vector is 390 km per hour N52.1 E