Question

a) Find the Velocity of object B immediately after the collision b) Find the speed of object B immediately after the collision c) Find the direction of object B immediately after the collision,giving the answer as an angle from the positive x axis in degrees to 1 decimal placed) Find the direction of object B immediately after the collision,giving the answer as bearing in degrees to 1 decimal place

Answer 1

Given:

the mass of the object A is

`m_A=2\text{ kg}`

The mass of the object B is

`m_B=4\text{ kg}`

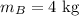
The velocity of the object A before the collision is

`u_A=-9i+11j\text{ m/s}`

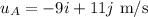
The velocity of the object B before the collision is

`u_B=i-j\text{ m/s}`

The velocity of the object A after the collision is

`v_A=-i+5j\text{ m/s}`

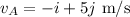
Required: the multiple parts to be solved

Step-by-step explanation:

to solve this problem, we will use momentum conservation.

according to the momentum conservation.

momentum before the collision = momentum after the collision.

we will conserve the momentum in the respective x and y directions.

the object A is the velocity in x and y direction is

`\begin{gathered} u_(Ax)=-9\text{ m/s} \\ u_(Ay)=11\text{ m/s} \end{gathered}`

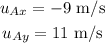
The object B velocity in the x and y direction is

`\begin{gathered} u_(Bx)=\text{ 1 m/s} \\ u_(By)=-1\text{ m/s} \end{gathered}`

(a)

momentum conservation in x direction is

momentum before the collision = momentum after the collision

`\begin{gathered} P_(ix)=P_(fx) \\ m_Au_(Ax)+m_Bu_(Bx)=m_Av_(Ax)+m_Bv_(Bx) \end{gathered}`

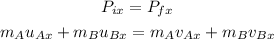
Plugging all the values in the above relation, we get:

`\begin{gathered} 2\text{ kg}*-9\text{ m/s }+4\text{ kg}*\text{1 m/s }=2\text{ kg}*-1\text{ m/s}+4\text{ kg}* v_(Bx) \\ v_(Bx)=-\text{ 3 m/s} \\ \end{gathered}`

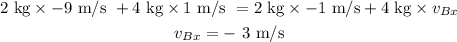
now apply momentum conservation in y direction,

`\begin{gathered} P_iy=P_(fy) \\ m_Au_(Ay)+m_Bu_(By)=m_Av_(Ay)+m_Bv_(BY) \end{gathered}`

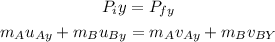
plugging all the values in the above relation, we get;

`\begin{gathered} 2\text{ kg}*11\text{ m/s}+4\text{ kg}*-1\text{ m/s }=2\text{ kg}*\text{5 m/s}+4\text{ kg}* v_(By) \\ v_(By)=2\text{ m/s} \end{gathered}`

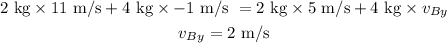
the velocity of the object B after the collision is

`\begin{gathered} v=v_(Bx)+v_(By) \\ v=-3i+2j\text{ m/s} \end{gathered}`

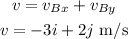
Thus, the velocity of the object B is

`v=-3\imaginaryI+2j\text{ m/s}`

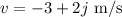
(b)

the speed of the object after the collision can be calculated as

`\begin{gathered} speed=\sqrt{v^2_{x^{\text{ }}}+v_y^2} \\ speed=√(-3^2+2^2) \\ speed=3.60\text{ m/s} \end{gathered}`

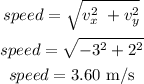
Thus, the speed of the object B is 3.60 m/s.

(c)

The direction of the object B can be found as,

the velocity of the object B after the collision is

'

`\begin{gathered} v_(Bx)=\text{ -3 m/s} \\ v_(By)=2\text{ m/s} \end{gathered}`

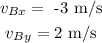
direction is given by

`\tan\theta=(v_(By))/(v_(Bx))`

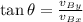
Plugging all the values in the above relation, we get:

`\begin{gathered} \tan\theta=\frac{2\text{ m/s}}{-3\text{ m/s}} \\ \theta=\tan^(-1)(-0.666) \\ \theta=123.24\text{ degree from the positive x axis} \end{gathered}`

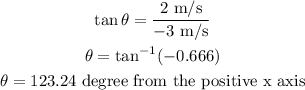
Thus, the direction is 123.24 degree.

(d)

f

The direction calculated as

`\begin{gathered} \tan\theta=\frac{2\text{ m/s}}{-3\text{ m/s}} \\ \tan\theta=-0.66 \\ \theta=33.24\text{ degree.} \end{gathered}`

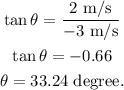
Thus, the direction is 33.24 degree.