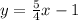Equation of a line
The slope-intercept form of the line can be written as follows:

Where m is the slope and b is the y-intercept
We have two points through which the line passes. If we substitute them into the equation, we can find the values of m and b.
Using the point (-4,-6):
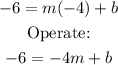
Using the point (4,4):
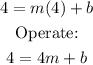
Subtract the second equation from the first equation:
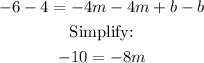
Solve for m:
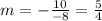
Substituting into the second equation:

Finally, the equation of the required line is: