We know the initial value of the car at time t = 0 and we know that it depreciates 9.7% per year.
If y is the value of the car and t is the time in years, we can write that:
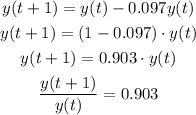
This correspond to an exponential decay model, that can be expressed as:
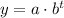
The parameter a can be calculated as:
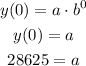
We can use the previous relationship to find the value of b:
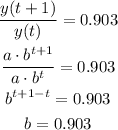
Then, we can express the value of the car after t years as:
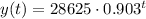
Then, after t = 10 years, the value is:
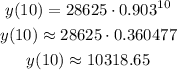
Answer: after 10 years, the value of the car is $10,318.65.