SOLUTION
Given the question in the question tab, the following are the solution steps to get the answer
Step 1: Write the given sides and angles
/(\sin A)=(b)/(\sin B)=(c)/(\sin C)]()
By substitution, we have

Step 3: To calculate length b using the sine rule;
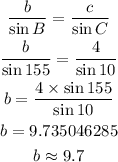
Therefore the sides of the first triangle becomes 6, 9.7 and 10 units while it’s angles are 15,10 and 155 degrees.
Step 4: Determine if there is another triangle
Also, if two sides are given as 6 units and 4 units respectively, then the third side can be calculated by using the Pythagoras theorem and this immediately presumes that it’s a right angled triangle (one of the angles equals 90 degrees). The theorem states that;

Taking the other two as 6 and 4 units, the formula now becomes;
![\begin{gathered} b^2=a^2+c^2 \\ b^2=6^2+4^2 \\ b^2=36+16 \\ b=\sqrt[]{42} \\ b=6.480740698 \\ b\approx6.48^(\circ) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uwwlkgfl8zufb5tphaym8vq5gr8e81bxmn.png)
Therefore the sides of the second triangle becomes 6, 6.48 and 4 units with angles as 10, 80 and 90 degrees.