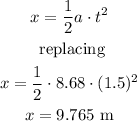ANSWER:
a) 8.68 m/s^2
b) 71.74 rad/s^2
c) 9.765 m
Explanation:
Given:
m1 = 2.85 kg
m2 = 0.742 kg
r = 0.121 m
a)
From the Newton's second law of motion, the downward force acting on the bucket is:
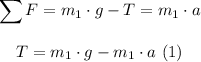
Torque acting on the pulley is:
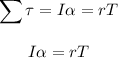
Hence, the angular acceleration is:
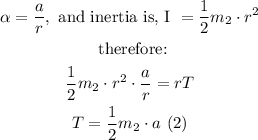
We equate equations (1) and (2), and solve for the acceleration like this:
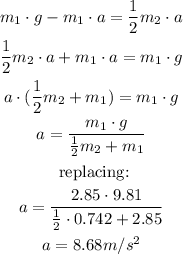
b)
The angular acceleration of the pulley is:
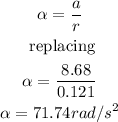
c)
We use the following equation to be able to calculate the distance: