Find the slope of a line that is perpendicular to the line 10x + 5y = 10. Round your answer to the nearest hundredth, if necessary.

Question

asked Nov 4, 2023 205k views

1 Answer

Varro · Answer 1 · 2023-11-08T06:18:59+0000

The line

Can be written as:

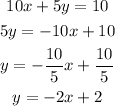
$\begin{gathered} 10x+5y=10 \\ 5y=-10x+10 \\ y=-(10)/(5)x+(10)/(5) \\ y=-2x+2 \end{gathered}$

This is the same line in the slope-intercept form:

Then, the original line has an slope of -2.

To find the slope of a perpendicular line to this one we need to remmeber that two lines are perpendicular if and only if

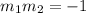
$m_1m_2=-1_{}_{}$

Plugging the value of the original line we have:

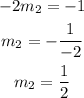
$\begin{gathered} -2m_2=-1 \\ m_2=-(1)/(-2) \\ m_2=(1)/(2) \end{gathered}$

Therefore a line perpendicular to the line 10x+5y=10 has slope 1/2 or 0.5.