Question

Please help with the problem. The equation given was
`g(x) = 3 \sin(2x) - 1`

Answer 1

The general equation is

`f(x)=A\sin (B(x+C))+D`

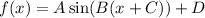
where A is the amplitude, the phase shift is C (if it is positive the shift is to the left), D is the vertical shift and the period is given as:

`(2\pi)/(B)`

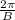
In this case we have the function:

`g(x)=3\sin (2x)-1`

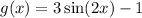
From this we notice that A=3, B=2, C=0 and D=-1; therefore:

Amplitude: 3

Phase shift is zero.

The vertical displacement is -1, this means that the function is translated vertically one unit down.

The period is:

`(2\pi)/(2)=\pi`

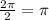
The equation of the midline is:

`y=-1`

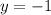
The graph of the function is shown below:

here the red graph is the sine function, the blue graph is the function g and the green line is the midline.