Question

A company manufactures and sells bookcases. The selling price is 53.9 (in dollars) per bookcase. The total cost function is linear, and costsamount to 50,000 (in dollars) for 2000 bookcases and 32, 120 (in dollars) for 800 bookcases.Find the break-even point.

Answer 1

Based on the problem, here are the given data:

Price per bookcase = $53.9

Cost amount for 2000 bookcase = $50,000

Cost amount for 800 bookcase = $32, 120

Let's assume the following variable:

x = the number of bookcases

y = the price per bookcase

Therefore, based on the problem, we have the following points for the cost function: (2000, 50000) and (800, 32120).

To solve for the break-even point, let's solve first the total cost function using the two-point formula.

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)_{}`

Using the points we have above, let's substitute them with the formula.

`\begin{gathered} y-50000=(32120-50000)/(800-2000)(x-2000) \\ y-50000=(-17880)/(-1200)(x-2000) \\ y-50000=14.9(x-2000) \\ y-50000=14.9x-29800 \\ y=149.9x-29800+50000_{} \\ y=14.9x+20200 \end{gathered}`

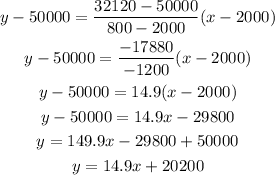
The total cost linear function is y = 14.9x + 20,200

Now, the break-even point is where the cost and income are equal.

Since it's given that the price per bookcase is 53.9, then we can say that the income is 53.9x in which x is the number of bookcases.

As mentioned, cost and income must be equal to determine the break-even point, therefore:

`53.9x=14.9x+20,200`

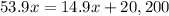
So, let's solve for x.

`\begin{gathered} 53.9x-14.9x=20,200 \\ 39x=20,200 \\ (39x)/(39)=(20,200)/(39) \\ x\approx517.95 \end{gathered}`

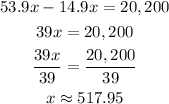
Therefore, at approximately 518 bookcases sold, the company will reach its break-even point.

At 518 bookcases sold, the company will have an income of $27, 920.20 since one bookcase is $53.9.

Using the total cost function, at 518 bookcases manufactured, the company's cost is y = 14.9(518) + 20, 200 = 7718.2 + 20, 200 = $27,918.20

Though we can see that the income is greater than 2 with the cost, that is because the exact number of bookcases must be 517.95, however, a number of bookcases cannot have a decimal value because it is a countable variable. It is