Compound inequality with "Or” indicates that, if one statement is true, the entire compound sentence is true.
1) So, let's evaluate each inequality:
(A)
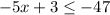
Isolating x:
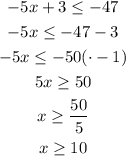
(B)
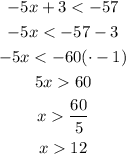
As we can see, the solution of equation A contains also the solution of equation B.
Also, in "Or” inequalities, it is only necessary that one statement is true. So, if statement A is true, the inequality is solved.
Answer:
{x ∈ R/x ≥ 10} or [10,∞)
Graph: