Question

Determine the equation of the line that passes through the point (1/5,−8) and is perpendicular to the line 5y−8x=−8.

Answer 1

`y=-(5)/(8)x-(63)/(8)`

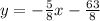
Explanation:

We have the equation of the following line:

`\begin{gathered} 5y−8x=−8 \\ \\ \text{ We solve for and to determine the slope:} \\ \\ 5y=-8+8x \\ \\ y=-(8)/(5)+(8)/(5)x \\ \\ y=(8)/(5)x-(8)/(5)\rightarrow y=mx+b \\ \\ \text{ therefore:} \\ \\ m=(8)/(5) \end{gathered}`

We have that when two lines are perpendicular, the product of their slopes is equal to -1, in this way we calculate the slope of the desired line:

`\begin{gathered} m_1\cdot m_2=-1 \\ \\ \text{ we replacing} \\ \\ (8)/(5)\cdot m_2=-1 \\ \\ m_2=-(5)/(8) \end{gathered}`

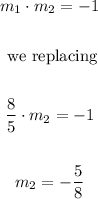
Now with the slope and the point (1/5, −8), we calculate the y-intercept to later determine the equation of the line just like this:

`\begin{gathered} -8=-(5)/(8)\cdot(1)/(5)+b \\ \\ -8=-(1)/(8)+b \\ \\ b=-8+(1)/(8) \\ \\ b=-(63)/(8) \\ \\ \text{ The equation would be:} \\ \\ y=-(5)/(8)x-(63)/(8) \end{gathered}`