Question

I need help with this practice problem I will show you a picture of my estimated answer later**

Answer 1

From the given angles, let's select the quadrant each of the angles drawn in the standard position lie.

We have the unit circle below:

Now, convert each of the given angles from radian to degrees and select the correct quadrant.

• From 0 to 90 degrees ==> Quadrant I

,

• From 91 to 180 degees ==> Quadrant II

,

• From 181 to 270 degrees ==> Quadrant III

,

• From 271 to 360 degrees ==> Quadrant IV

If the angle is greater than 360 subtract 360 from the angle until the angle is less than 360. If the angles is less than 0(negative), add 360 to the angle unitil the angle is between 1 and 360.

Thus, we have:

`\begin{gathered} (3\pi)/(4)\cdot(180)/(\pi)=135^o\Longrightarrow\text{ Quadrant II} \\ \\ (57\pi)/(8)*(180)/(\pi)=1282.5-1080=202.5^o\Longrightarrow\text{ Quadrant III} \\ \\ \end{gathered}`

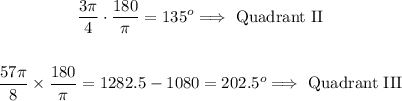
Solving further:

`\begin{gathered} (13\pi)/(6)*(180)/(\pi)=390-360=30^0==>Quadrant\text{ I} \\ \\ \\ -(35\pi)/(4)*(180)/(\pi)=-1575+360(4)=225^o\Longrightarrow Quadrant\text{ III} \\ \\ \\ -(5\pi)/(6)*(180)/(\pi)=-150+360=210^0\Longrightarrow Quadrant\text{ III} \\ \\ \\ -(5\pi)/(11)*(180)/(\pi)=-81.81+360=278.19^o\Longrightarrow Quadrant\text{ IV} \end{gathered}`

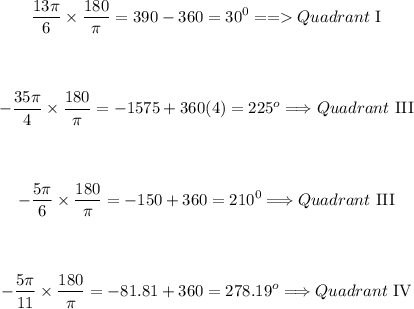
Therefore, the quandrant each angle lies is:

`\begin{gathered} (3\pi)/(4)\Longrightarrow Quadrant\text{ II} \\ \\ (57\pi)/(8)\Longrightarrow\text{ Quadtant III} \\ \\ (13\pi)/(6)\Longrightarrow\text{Quadrant I} \\ \\ -(35\pi)/(4)\Longrightarrow\text{ Quadrant III} \\ \\ -(5\pi)/(6)\Longrightarrow Quadrant\text{ III} \\ \\ -(5\pi)/(11)\Longrightarrow\text{Quadrant IV} \end{gathered}`