Question

A particle with a mass of 3.0 kg is accelerated due to a force with components Fx = 2N, Fy = 5N as shown in the figure. If the particle starts at rest, what is the total displacement of the particle after 10 seconds? In other words, what is the total distance traveled?

Answer 1

Given data:

* The x-component of force is,

`F_x=2\text{ N}`

* The y-component of force is,

`F_y=5\text{ N}`

* The mass of the particle is 3 Kg.

* The time taken by the particle is 10 seconds.

Solution:

According to the Newton's second law,

`F=ma`

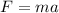
where a is the acceleration of the body,

For x-direction motion of the particle,

`\begin{gathered} F_x=ma_x \\ a_x=(F_x)/(m) \\ a_x=(2)/(3) \\ a_x=0.67ms^(-2) \end{gathered}`

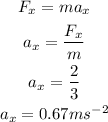
By the kinematics equation, the x-component of the displacement of particle is,

`\begin{gathered} d_x=(1)/(2)a_xt^2 \\ d_x=(1)/(2)*0.67*(10)^2 \\ d_x=33.5\text{ m} \end{gathered}`

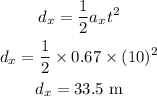
Similarly, for the motion of partcile along the y-direction is,

`\begin{gathered} F_y=ma_y \\ a_y=(F_y)/(m) \\ a_y=(5)/(3) \\ a_y=1.67ms^(-2) \end{gathered}`

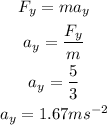
Thus, by the kinematics equation, the displacement of partcile along the y-direction is,

`\begin{gathered} d_y=(1)/(2)a_yt^2 \\ d_y=(1)/(2)*1.67*(10)^2 \\ d_y=83.5\text{ m} \end{gathered}`

Thus, the net distance traveled by the particle is,

`\begin{gathered} d=\sqrt[]{d^2_x+d^2_y} \\ d=\sqrt[]{33.5^2+83.5^2} \\ d=89.96\text{ m} \\ d\approx90\text{ m} \end{gathered}`

Hence, the total distance traveled by the particle is 90 m.