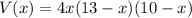Question

3. What are the roots of V(x)? What do the roots mean in this context? 4. Find the maximum volume of the box. What value of x gives the maximum volume? 5. Write V(x) in standard form and factored form.

Answer 1

1. To find the function that gives the volume, we will use the formula for the volume:

`V=l\cdot w\cdot h`

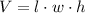
So, if the squares have sides x, the width will be to total of 20 minus the meqasures of the square, that is, minus 2x:

`w=20-2x`

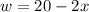
Similarly, the length will be the original length of 26 minus two sides of x, so:

`l=26-2x`

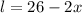
And the height is equal to one side of the square, so:

`h=x`

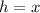
Then, the volume is:

`V=(26-2x)\cdot(20-2x)\cdot x`

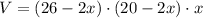
To simplify, we distribute the two parenthesis first:

`\begin{gathered} V(x)=(26-2x)\cdot(20-2x)\cdot x \\ V(x)=(26\cdot(20)+26\cdot(-2x)-2x\cdot(20)-2x\cdot(-2x))\cdot x \\ V(x)=(520-52x-40x+4x^2)\cdot x \\ V(x)=(520-92x+4x^2)\cdot x \\ V(x)=520x-92x^2+4x^3 \\ V(x)=4x^3-92x^2+520x \end{gathered}`

3. To find the roots of V(x), we need to find the values of xsuch that V(x) is zero. We could factor x out to get a quadratic equation and use the quadratic formula to find the roots. However, the function before we simplify is already factored in a way we can use to find the roots:

`\begin{gathered} V(x)=(26-2x)\cdot(20-2x)\cdot x \\ V(x)=(2\cdot13-2\cdot x)\cdot(2\cdot10-2\cdot x)\cdot x \\ V(x)=2(13-x)\cdot2(10-x)\cdot x \\ V(x)=2\cdot2\cdot x\cdot(13-x)(10-x) \\ V(x)=4x(13-x)(10-x) \end{gathered}`

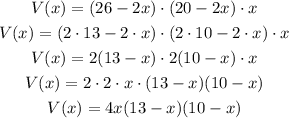
Now, we have the function in the factored form. The function will be zero when either of the factor are zero, so we have three possibilities:

`\begin{gathered} 4x=0\Rightarrow x=0 \\ 13-x=0\Rightarrow x=13 \\ 10-x=0\Rightarrow x=10 \end{gathered}`

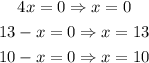
These roots, in this case, means that one of the dimensions of the box became zero.

When x = 0, the squares have zero dimensions, so there are no squares and this makes the height of the box to be zero, so it has 0 volume.

When x = 13, the side of the square is 13, which means it reaches the middle of the length of 26. Since we have one square on each side, this means that we will remove all the length, so the box will have zero length and thus 0 volume.

Similarly, when x = 10, the two squares wil reach the middle of the width, so all the width will be removed, making the volume 0 again.

These zeros could also be obtained by the graph, looking at x values of the points where the graph intercepts the x-axis:

4. By the graph, the maximum is infinite, because after the minimum, the graph grows indefinetely.

However, this don't make sense for this case, because this would mean that the x value is greater than half the length we have.

So, we can look at the maximum in the pick of the graph. From the graph, we can see that the point of maximum is at approximately (3.737, 867.196):

This means that the maximum volume is the y value of this point and this happens when x is the x value of this point.

So, the maximum volume is about 867.196 cm³ and this happens when x is about 3.737 cm.

5. We already did both of them.

The standard form is:

`V(x)=4x^3-92x^2+520x`

And the factored form is:

`V(x)=4x(13-x)(10-x)`