Given that an American family of four washes an average of
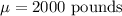
The standard deviation of the distribution is
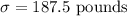
In order to find the probability that the mean off a randomnly selected sample of 50 families of 4 will be between 1,984 and 1992 pounds, you need to find the Z-scores.
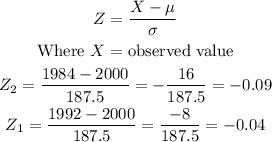
Hence, the probability would be:
[tex]\begin{gathered} Pr(Z_1