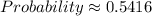Given that:
- The tread life of a particular tire design is normally distributed.
- The Mean (in miles) is:
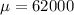
- The Standard Deviation (in miles) is:
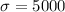
a. You need to find:

You need to find the corresponding z-score using this formula:
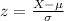
In this case:
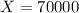
Therefore, by substituting values and evaluating, you get:
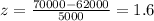
Then, you need to find:
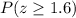
Using the Standard Normal Distribution Table, you get that:
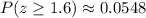
Therefore:
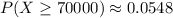
b. You need to find:
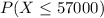
Find the z-score using:
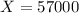
You get:
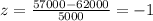
Then, you need to find the following using the Standard Normal Distribution Table:
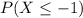
You get:
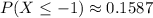
Therefore:
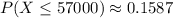
c. You need to find:
![P(57500Find the corresponding z-score for:[tex]X=57500](https://img.qammunity.org/2023/formulas/mathematics/college/sjuswx27dytvlfymfumzsxbtlinqwlybyv.png)
This is:
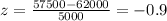
And find the z-score using:
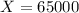
You get:
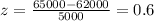
You need to find:
![P(-0.9Using the Standard Normal Distribution Table, you get that:[tex]P(z<0.6)\approx0.7257](https://img.qammunity.org/2023/formulas/mathematics/college/zpsu0ryt43xer3ekt1474yn8at5gv416x0.png)
And:
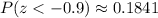
Therefore:
![P(-0.9Then:[tex]P(57500Hence, <strong>the answers are:</strong><p><strong>a.</strong></p>[tex]Probability\approx0.0548](https://img.qammunity.org/2023/formulas/mathematics/college/pjvpx75wfhf2e01l2iwwufwpddl3ftqpfd.png)
b.
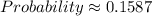
c.