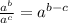Question

1) when raising a product to a power, raise each _______ to the power.2) when multiplying like bases, keep the base and _______ the exponents.3) when raising a power to a power, keep the base and _______ the exponents.4) any nonzero term raised to the _______ power is equal to 1.5) when raising a quotient to a power, raise the numerator and the _______ to the power6) when divining like bases, keep the base and _______ the exponents.choices: add, denominator, divide, exponent, factor, first, multiply, subtract, numerator, zero

Answer 1

Each statement refers to a mathematical property.

In order to correctly fill the empty spaces of the statements, we need to use the following words:

1) when raising a product to a power, raise each factor to the power.

Property:

`(a\cdot b)^c=a^c\cdot b^c`

2) when multiplying like bases, keep the base and add the exponents.

Property:

`a^b\cdot a^c=a^(b+c)`

3) when raising a power to a power, keep the base and multiply the exponents.

Property:

`(a^b)^c=a^(b\cdot c)`

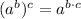
4) any nonzero term raised to the zero power is equal to 1.

Property:

`\begin{gathered} a^0=1 \\ a\\e0 \end{gathered}`

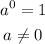
5) when raising a quotient to a power, raise the numerator and the denominator to the power.

Property:

`((a)/(b))^c=(a^c)/(b^c)`

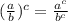
6) when divining like bases, keep the base and subtract the exponents.

Property:

`(a^b)/(a^c)=a^(b-c)`