Question

Fluorine exerts a pressure of 58 atm on a piston. When the pressure is changed to 89 atm, its volume is 64 mL. What was the original volume in mL?

Answer 1

We assume an isothermal and closed system, that is to say that there is no change in temperature and that no matter enters or leaves, therefore the number of moles remains constant.

We have an initial state and a final state. For the final state we are given the pressure and the volume. Using the ideal gas law we can find the relationship between moles and temperature. Since these two properties remain constant we can replace the relation in the initial state and find the volume of the fluorine.

Initial state:

P1= 58 atm

V1=?

Final state:

P2=89atm

V2=64 mL

So let's see what the ideal gas law is:

`PV=nR_{}T`

Where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is a constant

So, we have:

`\begin{gathered} P_1V_1=nR_{}T \\ P_2V_2=nR_{}T \\ \end{gathered}`

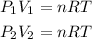
We can equal both equations:

`P_1V_1=P_2V_2`

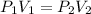
We clear V1, and replace known data:

`\begin{gathered} V_1=(P_2V_2)/(P_1) \\ V_1=\frac{89\text{atm}*64mL}{58atm}=98mL \end{gathered}`

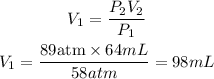
The original volume in mL was 98mL