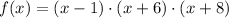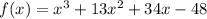
We can immediately check that f(1) = 0. Then we can divide the polynomial function by (x - 1):
x³ + 13x² + 34x - 48 | x - 1
-x³ + x² | x²
14x² + 34x - 48 | x - 1
-14x² + 14x | x² + 14x
48x - 48 | x - 1
-48x + 48 | x² + 14x + 48
Then we have:
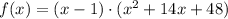
Now, we must find the roots of the quadratic term:
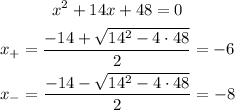
Therefore, we have: