Question

A jogger takes 4.5 minutes to run the same distance that a second jogger can run in 3.5 minutes. What is the distance if the second jogger runs 1.5 ft./sec. faster than the first jogger?(Explain)

Answer 1

Formula of speed, distance and time is:

`\text{speed}=\frac{dis\tan ce\text{ }}{time}`

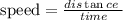
Let distance is:

`x`

Speed of first jogger is:

`S`

For first jogger :

`\begin{gathered} \text{speed}=(dis\tan ce)/(time) \\ S=(x)/(4.5) \end{gathered}`

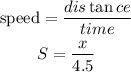
For the second jogger distance is same (x) and time is 3.5 minutes and speed is 1.5 then distance is:

`\begin{gathered} \text{time}=3.5*60 \\ =210\sec \text{.} \end{gathered}`

`\begin{gathered} \text{speed}=(dis\tan ce)/(time) \\ 1.5=(x)/(210) \\ x=210*1.5 \\ x=315\text{ ft} \end{gathered}`

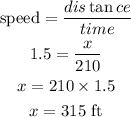
If distance is 315 ft then speed of first jogger is:

`\begin{gathered} \text{time}=4.5*60\text{ } \\ =270\text{ sec.} \end{gathered}`

`\begin{gathered} \text{speed}=(dis\tan ce)/(time) \\ S=(x)/(270) \\ S=(315)/(270) \\ S=1.16\text{ ft./sec.} \end{gathered}`

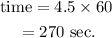
Second jogger is faster then first jogger then difference between speed is:

`\text{Faster sp}eed\text{ =spe}ed\text{ of second jogger - sp}eed\text{ of first jogger}`
`\begin{gathered} =1.5-1.16 \\ =0.34\text{ ft./sec.} \end{gathered}`

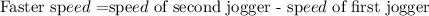
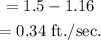
The second jogger is faster 0.34 ft/sec. then the first jogger.