Question

I don't know what to plug in, and the video links are not helpful.

Answer 1

Consider the general term,

`a_n=2+6n`

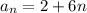
Substitute 0, 1, 2, 3 to get the first 4 terms of the series,

`2,8,14,20,\ldots\text{.}`

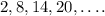
Consider that the difference between any two successive terms is constant at 6.

So this series will definitely form an arithmetic sequence.

So, it is a YES for the first box.

As already calculated the terms corresponding to n=0 is 2.

So the first term is 2.

Also the common difference is calculated by subtracting any term from its succeeding term,

`\begin{gathered} d=a_(n+1)-a_n \\ d=2+6(n+1)-\mleft\lbrace2+6n\mright\rbrace \\ d=2+6n+6-2-6n \\ d=6 \end{gathered}`

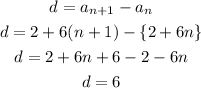
Thus the common difference is 6.