Question

Refer to the diagram in the picture A) what is the domain of the relationB) what is the range of the relationC) is the relation a function D) is the relation a one to one function

Answer 1

The domain of a function is the complete set of values of the independent variable (x), it means the values in the x axis where the relation exists. So in this case the domain is

`\lbrack-3;\infty)`

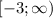
The range of a function is the complete set of values of the dependent variable (y). In this case the range of the relation includes all real numbers. So

`(-\infty;\infty)`

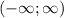
A function is a relation in where for each value of the independent variable (x), corresponds only a single value of the dependent variable (y). In this case for some values of x, corresponds two values of y, so this relation is not a function.

Finally to determine if it is a one to one function you can draw an horizontal line through the graph and check if it intersects the graph more than one. In this case the line does not intersect more than one, so it is a one to one function.