We have the expression:
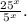
Using the distributive property for exponents, we write the expression as:
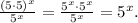
A)
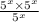
From the form above we see that this expression is equivalent.
B)
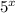
From the form above we see that this expression is equivalent.
C) We have the expression:
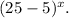
Simplifying this expression, we have:
s