Question

Hello, I’m stuck on a practice problem… I need to show all work.

Answer 1

`t\approx1.14secs`

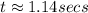
Explanations:

Givenhthe equation ofthe height rcoveredby the ball expressed as:

`h(t)=-16t^2+5t+15`

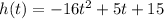
The height of the ball on the ground is zero that is h(t) = 0. Substitute into the equation to determine the required time.

`\begin{gathered} -16t^2+5t+15=0 \\ 16t^2-5t-15=0 \end{gathered}`

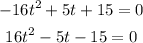
Factorise the esult using the quadratic frormula

`\begin{gathered} t=(-b\pm√(b^2-4ac))/(2a) \\ t=(-(-5)\pm√((-5)^2-4(16)(-15)))/(2(16)) \\ t=(5\pm√(25+960))/(32) \\ t=(5\pm√(985))/(32) \\ t=(5+31.39)/(32) \\ t=(36.39)/(32) \\ t=1.14seconds \end{gathered}`

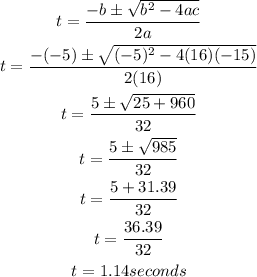
Hence it will take the ball approximately 1.14seconds to hit the ground