Question

The distance between the two points P (15,x)and Q(x,-5)is 20.

Answer 1

x = - 5, x = 15

Explanation:

Assuming you require to find the values of x

Calculate the distance PQ using the distance formula and equate to 20

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-x_(1))^2 }`

with (x₁, y₁ ) = P (15, x ) and (x₂, y₂ ) = Q (x, - 5 )

PQ =
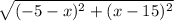`√((-5-x)^2+(x-15)^2)` = 20 ( square both sides )

(- 5 - x)² + (x - 15)² = 20² ← expand factors on left side using FOIL

25 + 10x + x² + x² - 30x + 225 = 400

2x² - 20x + 250 = 400 ( subtract 400 from both sides )

2x² - 20x - 150 = 0 ( divide through by 2 )

x² - 10x - 75 = 0

consider the factors of the constant term (- 75) which sum to give the coefficient of the x- term (- 10)

the factors are - 15 and + 5 , since

- 15 × 5 = - 75 and - 15 + 5 = - 10 , then

(x - 15)(x + 5) = 0

equate each factor to zero and solve for x

x + 5 = 0 ⇒ x = - 5

x - 15 = 0 ⇒ x = 15