The gravitation field strength is given as,
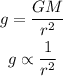
Here, G is the universal gravitational constant, M is the mass of the planet, and r is the separation between the center of the planet and the object.
Now, when the object is moved 1000 m away from the surface, so the new separation between the center of the planet and the object is,
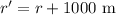
From the above equation, it is clear that r'>r.
The new gravitational field strength 1000 m away from the surface is,
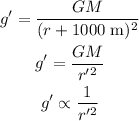
Since, r'>r. Hence, g>g'. Therefore, the gravitational field strength of the planet is smaller at a distance of 1000 m away from the surface, than the gravitational field strength at the surface.