Question

#15 approximate the length support to the neares tenth of a foot

Answer 1

Given:

a triangle is given as below

Find:

we have to find the length of the vertical support.

Step-by-step explanation:

Firstly we will find the area of triangle using Heron's formula as below

`Area=√(s(s-a)(s-b)(s-c))`

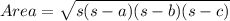
where 's' is semi-perimeter of the triangle.

`s=(13.6+4.4+14.3)/(2)=16.15\text{ }ft`

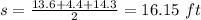
Therefore, area of the given triangle is

`\begin{gathered} Area=√(16.15(16.15-13.6)(16.15-4.4)(16.15-14.3)) \\ Area=√(16.5*2.55*11.75*1.85) \\ Area=√(914.6053125) \\ Area=30.24\text{ }ft^2(approximately) \end{gathered}`

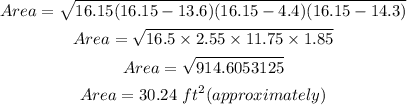
Let 'x' be the length of the vertical support (which is height of the triangle)

Now, area of a triangle is equal to (1/2)*base*height.

`\begin{gathered} 30.24=(1)/(2)*14.3* x \\ x=(30.24*2)/(14.3) \\ x=4.2\text{ }ft(approximately) \end{gathered}`

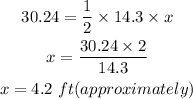
Therefore, The approximate length of the support is about 4.2 ft.

So, C is the correct option.