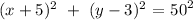1 Answer

Rubia Gardini · Answer 1 · 2023-12-24T03:49:44+0000

Let’s find the equation of a circle with

radius r and center (-5,3)=(h,k) and that passes through (0,-2):

By definition, an equation of the circle with center (h,k) and radius r is:

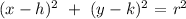
$(x-h)^2\text{ }+\text{ (}y-k)^2\text{ = }r^2$

This is called the standard form for the equation of the circle. So, in our case we would have:

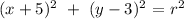
$(x+5)^2\text{ }+\text{ (}y-3)^2\text{ = }r^2$

Now, if we have the point (x,y) = (0,-2), we resolve the above equation for radius r. That is:

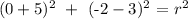
$(0+5)^2\text{ }+\text{ (-2}-3)^2\text{ = }r^2$

that is equivalent to say:

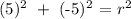
$(5)^2\text{ }+\text{ (-5})^2\text{ = }r^2$

that is equivalent to

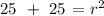
$25^{}\text{ }+\text{ 25}^{}\text{ = }r^2$

that is:

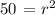
$50^{}\text{ = }r^2$

so, replacing the radius previously found, as well as the center of the circle, in the canonical equation of the circle we obtain:

$r\text{ = }\sqrt[]{50}\text{ = 5}\sqrt[]{2}$

replacing the radius previously found, as well as the center of the circle, in the canonical equation of the circle we obtain:

$(x+5)^2\text{ }+\text{ (}y-3)^2\text{ = 50}^2\text{ = 5}\sqrt[]{2}$

so, the correct equation for the circle is

$(x+5)^2\text{ }+\text{ (}y-3)^2\text{ = 50}^2\text{ }$

Please log in or register to add a comment.