Question

If (x, y) is a point on the circle x² + y² = 1 and the distance from the point P(x, y) to (-1,0) is

d = 4/5, then find the x-coordinate of point P exactly

Answer 1

First, let's use the distance formula to calculate the distance between P and (-1, 0):

`\begin{gathered} d=√((y_2-y_1)^2+(x_2-x_1)^2)\\ \\ d=√((0-y)^2+(-1-x)^2)\\ \\ (4)/(5)=√(y^2+x^2+2x+1) \\ ((4)/(5))^2=x^2+y^2+2x+1 \end{gathered}`

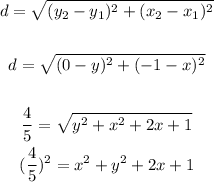
Since point P is on the given circle, let's subtract the equation above from the circle equation, then we solve the resulting equation for x:

`\begin{gathered} x^2+y^2+2x+1-(x^2+y^2)=((4)/(5))^2-(1)\\ \\ 2x+1=(16)/(25)-1\\ \\ 2x=(16)/(25)-2\\ \\ x=(8)/(25)-1=(8)/(25)-(25)/(25)=-(17)/(25) \end{gathered}`

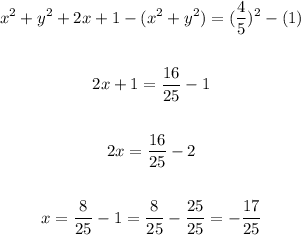
Therefore the x-coordinate of P is -17/25.