Question

Find the height of the tree if the tree's shawdow is 24 feet, the stick person's height is 5 feet, and the stick person's shadow is 8 feet.

Answer 1

The height of the tree and its shadow, and the height of the person and its shadow, at the same time of the day, form two similar right triangles:

Since both triangles are similar, then the corresponding sides are at the same ratio so that:

`\begin{gathered} \frac{\text{height tree}}{\text{height person}}=\frac{shadow\text{ tree}}{shadow\text{ person}} \\ (x)/(5)=(24)/(8) \end{gathered}`

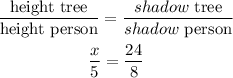
From this expression, you can determine the height of the tree, just multiply both sides of the equal sign by 5:

`\begin{gathered} 5\cdot(x)/(5)=5\cdot(24)/(8) \\ x=5\cdot3 \\ x=15ft \end{gathered}`

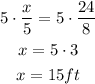
The height of the tree is 15 feet.