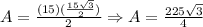Question

I have a final on this pls help number 7

Answer 1

We will have the following:

a. We can see that the angle opposite to x is 45° and the angle opposite to 10 is also 45°; from theorems [Congruent angles that oppose sides in a triangle have that those sides are also congruent]; so:

x = 10.

Now, we determine y using the law of sines:

`(y)/(sin(90))=(10)/(sin(45))\Rightarrow y=10√(2)`

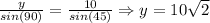
Now, we determine the height of the triangle:

`\begin{gathered} 10^2=(5√(2))^2+h^2\Rightarrow h^2=100-50 \\ \\ \Rightarrow h=5√(2) \end{gathered}`

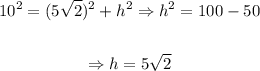
So, the perimeter is:

`P=10+10+10√(2)\Rightarrow P=20+10√(2)`

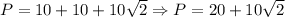
The area is:

`A=((10√(2))(5√(2)))/(2)\Rightarrow A=50`

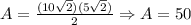
b. Same as in the previous triangle we will determine x and y:

x = 15

`(y)/(sin(60))=(15)/(sin(60))\Rightarrow y=15`

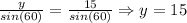
Now, we determine the height of the triangle:

`h=\sqrt{(15)^2-((15)/(2))^2}\Rightarrow h=(15√(3))/(2)`

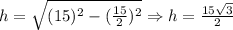
So, the perimeter is:

`P=15+15+15\Rightarrow P=45`

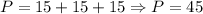
The area is:

`A=((15)((15√(3))/(2)))/(2)\Rightarrow A=(225√(3))/(4)`