Solution
- The question would like us to solve the following inequality:
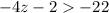
- The solution is given below:

- Thus, we need to put the solution in both Set-builder notation and Interval notation. This is done below:
Set-builder notation:
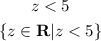
Interval notation:
