For this problem we have a right triangle WXV with the following info:
And we want to find: cot W
From definition we know that cotangent is the inverse of tangent and it's given by:
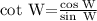
From the info given we can find cos W and sin W and we got:
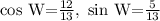
And then we can find the cotangent like this:
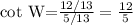
And then the final answer for this case would be cot