Let's take l and w as the length and the width of the rectangle.
According to the given information the length is 3 less than twice the width:

And the area, which is the product of the length times the width is 14. Using the equation above, we can re write the formula for the area, this way:
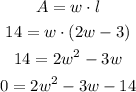
Now, we have to solve the quadratic equation using the quadratic formula:
![\begin{gathered} w=\frac{-(-3)\pm\sqrt[]{(-3)^2-4(2)(-14)}}{2(2)} \\ w=\frac{3\pm\sqrt[]{9+112}}{4} \\ w=\frac{3\pm\sqrt[]{121}}{4} \\ w=(3\pm11)/(4) \\ w1=(14)/(4)=(7)/(2) \\ w2=-(8)/(4)=-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6lyelxebz6vl3fbtqv3lr5wp2stzpczw2z.png)
w has 2 values, but for this context, the logic value is 7/2. It means that the width of the rectangle is 7/2.
Now, we can use this value and the first equation to find the length:
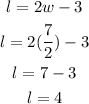
The length of the rectangle is 4 and the width is 7/2.