Given the following system of equations:
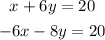
to solve by substitution, first notice that we can solve for x on the first equation to get the following:
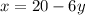
substituting this value on the second equation we get:
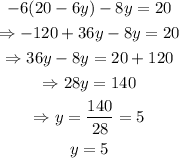
now that we have that y=5, we can find the value of x by using our first equation:
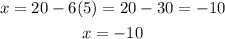
therefore, the solution is (-10,5)