Question

Reciprocal Formulas Using a Calculator will send pic

Answer 1

Step-by-step explanation:

In the equation

`(1)/(R)=(1)/(R_1)+(1)/(R_2)`

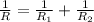
we out in R = 12 and R_2 = 21 to get

`(1)/(12)=(1)/(R_1)+(1)/(21)`

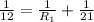
Subtracting 1/21 from both sides gives

`(1)/(12)-(1)/(21)=(1)/(R_1)`

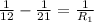
We subtract the fractions on the left-hand side to get

`(1\cdot21)/(12\cdot21)-(1\cdot12)/(21\cdot12)`
`=(9)/(252)=(1)/(28)`

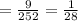
Hence,

`(1)/(28)=(1)/(R_1)`

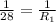
Taking the reciprocal of both sides gives

`R_1=28`

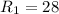
Which is our answer!