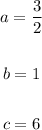Given the equation of a hyperbola:
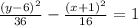
• You need to remember that the equation of a vertical hyperbola has this form:
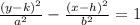
Where the center is:
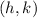
In this case, you can identify that:

Therefore, its Center is at this point:
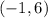
• By definition, the Vertices of a vertical hyperbola can be found with:

In this case, you know that:
![a=\sqrt[]{36}=\pm6](https://img.qammunity.org/2023/formulas/mathematics/college/e1zat7kxeqr8ai4gyvmni5i84q4vhr7cb4.png)
Therefore, you can determine that the Vertex with the larger y-value is:
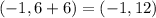
And the Vertex with the smaller y-value is:
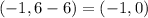
• By definition, the formula for calculating the distance from the Center of a hyperbola to the Foci is:
![c=\sqrt[]{a^2+b^2}](https://img.qammunity.org/2023/formulas/mathematics/college/6uwqakmkjq6nua21bpopztkrf20jt2flji.png)
You already know the value of "a", and you can determine that:
![b=\pm\sqrt[]{16}=\pm4](https://img.qammunity.org/2023/formulas/mathematics/college/lgftba3ita6rs19p7uekejr4bson3uj6y4.png)
Therefore, by substituting values into the formula and evaluating, you get:
![c=\sqrt[]{6^2+4^2}=2\sqrt[]{13}](https://img.qammunity.org/2023/formulas/mathematics/college/8h2i26azrn7yoc3811zfcjltbzdc0i0tro.png)
By definition, Focis of a vertical hyperbola have this form:

Hence, the Foci with a larger y-value is:
![(-1,6+2\sqrt[]{13})](https://img.qammunity.org/2023/formulas/mathematics/college/7hg3d4hd0bcdddw2qu4gmzmljd6r0w6qdh.png)
And the Foci with the smaller y-value is:
![(-1,6-2\sqrt[]{13})](https://img.qammunity.org/2023/formulas/mathematics/college/i257kg60c94w3nyb2097tcs887x13dfkix.png)
• According to the information provided in the exercise, one of the Asymptotes is the equation:

By definition, the equation for the Asymptotes of a vertical hyperbola is:
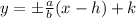
Knowing all the values, you get:
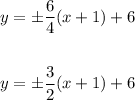
Hence, the answers are:
• Center:
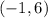
• Vertex with a larger y-value:
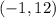
Vertex with a smaller y-value:
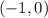
Foci with a larger y-value:
![(-1,6+2\sqrt[]{13})](https://img.qammunity.org/2023/formulas/mathematics/college/7hg3d4hd0bcdddw2qu4gmzmljd6r0w6qdh.png)
Foci with a smaller y-value:
![(-1,6-2\sqrt[]{13})](https://img.qammunity.org/2023/formulas/mathematics/college/i257kg60c94w3nyb2097tcs887x13dfkix.png)
Values of "a", "b" and "c" of the equation of one of the asymptotes: