Rate of change means the slope.
Intervals considered x = 0 to x = 3.
At x = 0:
f(x) = 3/2x + 2
f(x) = (3/2)(0) + 2
f(x) = 2
At x = 3:
f(x) = 3/2x + 2
f(x) = (3/2)(3) + 2
f(x) = 4.5 + 2
f(x) = 6.5
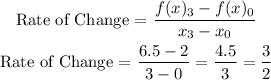
The average rate of change for f(x) is 3/2.
Let's now solve for the average rate of change of g(x).
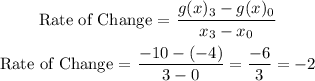
The average rate of change for g(x) is -2.
Comparing the two averages, f(x) is greater than g(x).
The answer is Option 1.