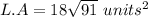Question

Find the lateral area the regular pyramid. The answer has to be in the format below LA

Answer 1

GIVEN:

We are given a regular pyramid with the following dimensions;

`\begin{gathered} Base=6 \\ \\ Height=8 \end{gathered}`

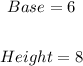
Required;

To calculate the lateral area.

Step-by-step solution;

To begin, we first take note that what we have is a regular pyramid with a hexagonal base. That is, the base has 6 sides.

Also, it is called a regular pyramid which means all sides of the base are equal.

We are given the formula for the lateral area as follows;

`\begin{gathered} For\text{ }a\text{ }hexagonal\text{ }pyramid: \\ \\ Lateral\text{ }Area=3a\sqrt{h^2+(3a^2)/(4)} \end{gathered}`

Where you have;

`\begin{gathered} a=base \\ \\ h=height \end{gathered}`

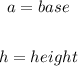
We now have;

`Lateral\text{ }Area=3(6)\sqrt{8^2+(3(6)^2)/(4)}`

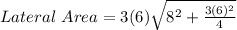
Now we can simplify;

`\begin{gathered} Lateral\text{ }Area=18\sqrt{64+(3(36))/(4)} \\ \\ Lateral\text{ }Area=18√(64+27) \\ \\ Lateral\text{ }Area=18√(91) \\ \\ Lateral\text{ }Area=171.709056255 \end{gathered}`

We can however write the "exact answer" as follows;

ANSWER:

`L.A=18√(91)\text{ }units^2`