We are given that the Titanic hit an iceberg half of its mass. To determine the velocity of the iceberg after the collision we have to do a balance of momentum:

Where:

Now, since the iceberg is initially at rest, we have:
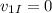
Substituting in the balance of momentum we get:
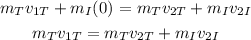
We are given that the mass of the iceberg is half of the mass of the Titanic, therefore, we have:
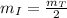
Substituting in the balance of momentum:

Now, we can cancel out the mass of the Titanic:
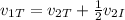
Now we solve for the final velocity of the iceberg. We subtract the final velocity of the Titanic from both sides:
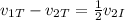
Now we multiply both sides by 2:
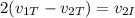
Substituting the values we get:
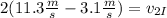
Solving the operations we get:

Therefore, the final velocity of the iceberg is 16.4 meters per second.