Question

Find the measure of each angle. Tell which postulate(s) or theorem(s) you used.3. m∠2

Answer 1

Both lines w and v are parallel.

They are intersected by the lines p and q forming several angles.

Let's start with the angles formed between w, v, and p

We know that m∠9=80º

1)

m∠9 and m∠10 are a linear pair over line "p", linear pairs are adjacent supplementary angles, which means that they add up to 180º

Knowing this we can calculate the value of m∠10 as follows:

`\begin{gathered} m\angle9+m\angle10=180 \\ m\angle10=180-m\angle9 \\ m\angle10=180-80 \\ m\angle10=100º \end{gathered}`

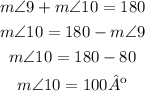
2)

Angles m∠2 and m∠10 are corresponding angles, if you see the lines between them are F shaped

Corresponding angles are congruent, so that

`m\angle10=m\angle2=100º`

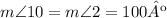
m∠2 measures 100º