Trigonometric Identities.
To solve this problem, we need to keep in mind the following:
* The tangent function is negative in the quadrant II
* The cosine (and therefore the secant) function is negative in the quadrant II
* The tangent and the secant of any angle are related by the equation:
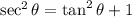
We are given:
![\text{tan}\theta=-\frac{\sqrt[]{14}}{4}](https://img.qammunity.org/2023/formulas/mathematics/high-school/qg11hgdg45s0eap4ma96z7t8dsrxnm2ww9.png)
And θ lies in the quadrant Ii.
Substituting in the identity:
![\begin{gathered} \sec ^2\theta=(-\frac{\sqrt[]{14}}{4})^2+1 \\ \text{Operating:} \\ \sec ^2\theta=(14)/(16)+1 \\ \sec ^2\theta=(14+16)/(16) \\ \sec ^2\theta=(30)/(16) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rxb0ifpr6s5018nlqamlnnh0z3ltwpfsk3.png)
Taking the square root and writing the negative sign for the secant:
![\begin{gathered} \sec ^{}\theta=\sqrt{(30)/(16)} \\ \sec ^{}\theta=-\frac{\sqrt[]{30}}{4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/g4dcqp542kysjl2o9wrmiva9xhbfp39qmg.png)