Question

State the composition of transformations used below that take △ABC to △ A" B" C" .

Answer 1

We have to identify the transformations that take △ABC to △A"B"C".

The first transformation takes △ABC to △A'B'C'. We can see that the triangle is reflected over the x-axis (horizontal axis).

For example, as C is located on the x-axis, C' is also located on the x-axis. For A and B, its vertical coordinates change sign but mantain its absolute value.

We can write this transformation as:

`(x,y)\longrightarrow(x,-y)`

This transformation shows that the horizontal coordinates are mantained and the vertical coordinates have their sign inverted.

The second transformation is a translation. The orientation stays the same but the points are translated a fixed number of units in both the horizontal and vertical direction.

We can take any point and its transformed point and compare its coordinates. For example B'' is 6 units to the right and 2 units up.

Then, we can write:

`B(-1,2)\longrightarrow B^(\prime)^(\prime)(5,4)`

We can generalize this to the rule:

`(x,y)\longrightarrow(x+6,y+2)`

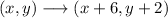
as the x-coordinate will increase 6 units and the y-coordinate will increase 2 units.

Answer: the transformations are a reflection over the horizontal axis (y=0) and a translation of (x+6,y+2) [First option].

​