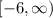We are given the following functions:
![\begin{gathered} f(x)=7\sqrt[]{x}+6 \\ g(x)=x+6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/jyvzsi0sjv30n16mg7lyi11y7dwrw7vaqx.png)
We are asked to determine the composite function:

The composition of functions is equivalent to:
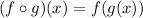
Therefore, we replace the value of "x" in function "f" for the function "g", therefore, we get:
![(f\circ g)(x)=f(g(x))=7\sqrt[]{x+6}+6](https://img.qammunity.org/2023/formulas/mathematics/high-school/7p5smsoqtdw521xsut0usxkwfuinsiba54.png)
Since we can't simplify any further this is the composition.
Now we are asked to determine the domain of this function. Since we have a square root, the domain must be the values of "x" where the term inside the radical is greater or equal to zero, therefore, we have:
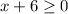
Now we solve for "x" by subtracting 6 from both sides:
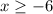
Therefore, the domain is: