Answer:
AM = 36, AB = 72
MN = 9, AC = 18
Step-by-step explanation:
Solving the equations of the previous problem, we find that x = 9 and y = 6.
Now we put these values in the expressions for the side lengths and find the length measures.
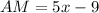
putting in x = 9 gives
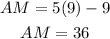
For AB we have
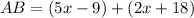
putting in x = 9 gives
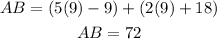
For MN we have
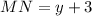
putting in y = 6 gives
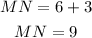
which is our answer!
For AC we have
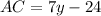
putting in y = 6 gives
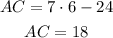
Hence, to summarise
AM = 36, AB = 72
MN = 9, AC = 18